 Introducción. Dados los vectores a y b linealmente independientes de E3(R) deseamos calcular todos los vectores que que son simultáneamente perpendiculares a a y b. En todo momento nos referimos a la base ortonormal { e1, e2, e3 } Introducción. Dados los vectores a y b linealmente independientes de E3(R) deseamos calcular todos los vectores que que son simultáneamente perpendiculares a a y b. En todo momento nos referimos a la base ortonormal { e1, e2, e3 }
Sean { a1, a2, a3 } y { b1, b2, b3 } las coordenadas de a y b respecto de la base dada y (x, y, z) las coordenadas de un vector genérico x que deseamos cumpla las condiciones de perpendicularidad que se han indicado.
Si dicho vector ha de ser perpendicual a a y b el producto escalar de cada uno de ellos por x es cero. Por tanto
siendo 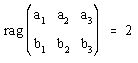 pues a y b linealmente independientes. Teniendo esto en cuenta resulta que el sistema anterior es compatible indeterminado con grado de indeterminación 1. Resolviéndolo, por ejemplo por el método de Crámer, resulta
Para el valor pues a y b linealmente independientes. Teniendo esto en cuenta resulta que el sistema anterior es compatible indeterminado con grado de indeterminación 1. Resolviéndolo, por ejemplo por el método de Crámer, resulta
Para el valor 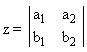 una solución es
que es una base del conjunto de vectores que son perpendiculares a a y b. (Evidentemente la dimensión de dicho subespacio es 1). una solución es
que es una base del conjunto de vectores que son perpendiculares a a y b. (Evidentemente la dimensión de dicho subespacio es 1).
 Definimos , teniendo en cuenta lo anterior, el producto escalar de los vectores a(a1, a2, a3) y b(b1, b2, b3), referidos a una base ortonormal { e1, e2, e3 } por Definimos , teniendo en cuenta lo anterior, el producto escalar de los vectores a(a1, a2, a3) y b(b1, b2, b3), referidos a una base ortonormal { e1, e2, e3 } por
 Las propiedades del producto vectorial enunciadas a continuación son inmediatas teniendo en cuenta las propiedades de los determinantes: Las propiedades del producto vectorial enunciadas a continuación son inmediatas teniendo en cuenta las propiedades de los determinantes:
- el producto escalar no es conmutativo;
-
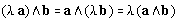
-
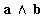 el ortogonal a a y a b (por construcción) el ortogonal a a y a b (por construcción)
-
 (siendo || a || la norma (o módulo) del vector a) (siendo || a || la norma (o módulo) del vector a)
-
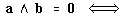 a y b son linealmente dependientes a y b son linealmente dependientes
- Si a y b son linealmente independientes entonces a, b y
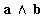 forman una base. forman una base.
|
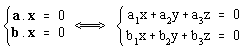
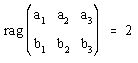 pues a y b linealmente independientes. Teniendo esto en cuenta resulta que el sistema anterior es compatible indeterminado con grado de indeterminación 1. Resolviéndolo, por ejemplo por el método de Crámer, resulta
pues a y b linealmente independientes. Teniendo esto en cuenta resulta que el sistema anterior es compatible indeterminado con grado de indeterminación 1. Resolviéndolo, por ejemplo por el método de Crámer, resulta
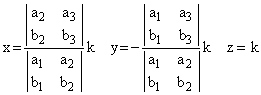
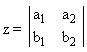 una solución es
una solución es
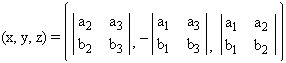
![]() Definimos , teniendo en cuenta lo anterior, el producto escalar de los vectores
Definimos , teniendo en cuenta lo anterior, el producto escalar de los vectores 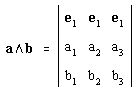
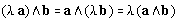
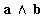 el ortogonal a a y a b (por construcción)
el ortogonal a a y a b (por construcción) (siendo
(siendo 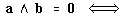 a y b son linealmente dependientes
a y b son linealmente dependientes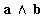 forman una base.
forman una base.

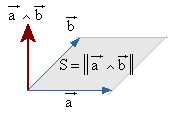 El producto vectorial tiene una sencilla e importante interpretación geométrica que facilita bastante problemas. La norma (o módulo) del vector producto vectorial es igual que el área del paralelogramo determinado por los vectores que lo definen.
El producto vectorial tiene una sencilla e importante interpretación geométrica que facilita bastante problemas. La norma (o módulo) del vector producto vectorial es igual que el área del paralelogramo determinado por los vectores que lo definen.
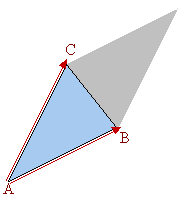 Ejemplo 1 Para calcular el área del triángulo de vértices
Ejemplo 1 Para calcular el área del triángulo de vértices 
 Regresa a la pagina principal
Regresa a la pagina principal